Determining the Number of Significant Figures
The number of significant figures in a measurement, such as 2.531, is equal to the number of digits that are known with
some degree of confidence (2, 5, and 3) plus the last digit (1), which is an estimate or approximation. As we improve the
sensitivity of the equipment used to make a measurement, the number of significant figures increases.
| Postage Scale |
|
3 ±1 g |
|
1 significant figure |
| Two-pan balance |
|
2.53 ±0.01 g |
|
3 significant figures |
| Analytical balance |
|
2.531 ±0.001 g |
|
4 significant figures |
Rules for counting significant figures are summarized below.
Zeros within a number are always significant. Both 4308 and 40.05 contain four significant figures.
Zeros that do nothing but set the decimal point are not significant. Thus, 470,000 has two significant figures.
Trailing zeros that aren't needed to hold the decimal point are significant. For example, 4.00 has three significant figures.
If you are not sure whether a digit is significant, assume that it isn't. For example, if the directions for an experiment
read: "Add the sample to 400 mL of water," assume the volume of water is known to one significant figure.
Addition and Subtraction with Significant Figures
When combining measurements with different degrees of accuracy and precision, the accuracy of the final answer can
be no greater than the least accurate measurement. This principle can be translated into a simple rule for addition and
subtraction: When measurements are added or subtracted, the answer can contain no more decimal places than the least
accurate measurement.
| 150.0 g H2O |
(using significant figures) |
| + 0.507 g salt |
| 150.5 g solution |
Multiplication and Division With Significant Figures
The same principle governs the use of significant figures in multiplication and division: the final result can be no more
accurate than the least accurate measurement. In this case, however, we count the significant figures in each measurement,
not the number of decimal places: When measurements are multiplied or divided, the answer can contain no more significant
figures than the least accurate measurement.
Example: To illustrate this rule, let's calculate the cost of the copper in an old penny that is pure copper. Let's assume
that the penny has a mass of 2.531 grams, that it is essentially pure copper, and that the price of copper is 67 cents per
pound. We can start by from grams to pounds.
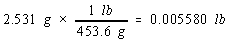
We then use the price of a pound of copper to calculate the cost of the copper metal.
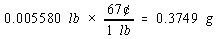
There are four significant figures in both the mass of the penny (2.531) and the number of grams in a pound (453.6). But there
are only two significant figures in the price of copper, so the final answer can only have two significant figures.
| Practice Problem 7
Calculate the length in inches of a piece of wood 1.245 feet long. Determine the correct number of significant figures.
Answer:
14.94 in |
Rounding Off
When the answer to a calculation contains too many significant figures, it must be rounded off.
There are 10 digits that can occur in the last decimal place in a calculation. One way of rounding off involves underestimating
the answer for five of these digits (0, 1, 2, 3, and 4) and overestimating the answer for the other five (5, 6, 7,
8, and 9). This approach to rounding off is summarized as follows.
If the digit is smaller than 5, drop this digit and leave the remaining number unchanged. Thus, 1.684 becomes 1.68.
If the digit is 5 or larger, drop this digit and add 1 to the preceding digit. Thus, 1.247 becomes 1.25.

